testOTM
testOTM is an R package that computes multivariate ranks and quantiles defined through the theory of optimal transportation. It also provides several applications of these statistics, most notably a method for two-sample multivariate goodness-of-fit testing.
Installation
You can install the released version of testOTM from CRAN with:
install.packages("testOTM")
You can install the development version from GitHub with:
# install.packages("devtools")
# devtools::install_github("Francis-Hsu/testOTM")
Example
This is a basic example which shows you how to use testOTM to visualize the optimal transport map from $U[0, 1]^2$ to a (scaled) bivariate normal sample:
library(testOTM)
# generate bivariate normal data
p = 2
n = 100
Sigma = matrix(c(2, 1, 1, 2), 2, 2)
eS = eigen(Sigma, symmetric = TRUE)
X = t(eS$vectors %*% diag(sqrt(pmax(eS$values, 0)), p) %*% matrix(rnorm(p * n), p))
# compute the optimal transport map from U[0, 1]^2 to the data
# notice that the data will be scale into [0, 1] range
X.OTM = tos.fit(X)
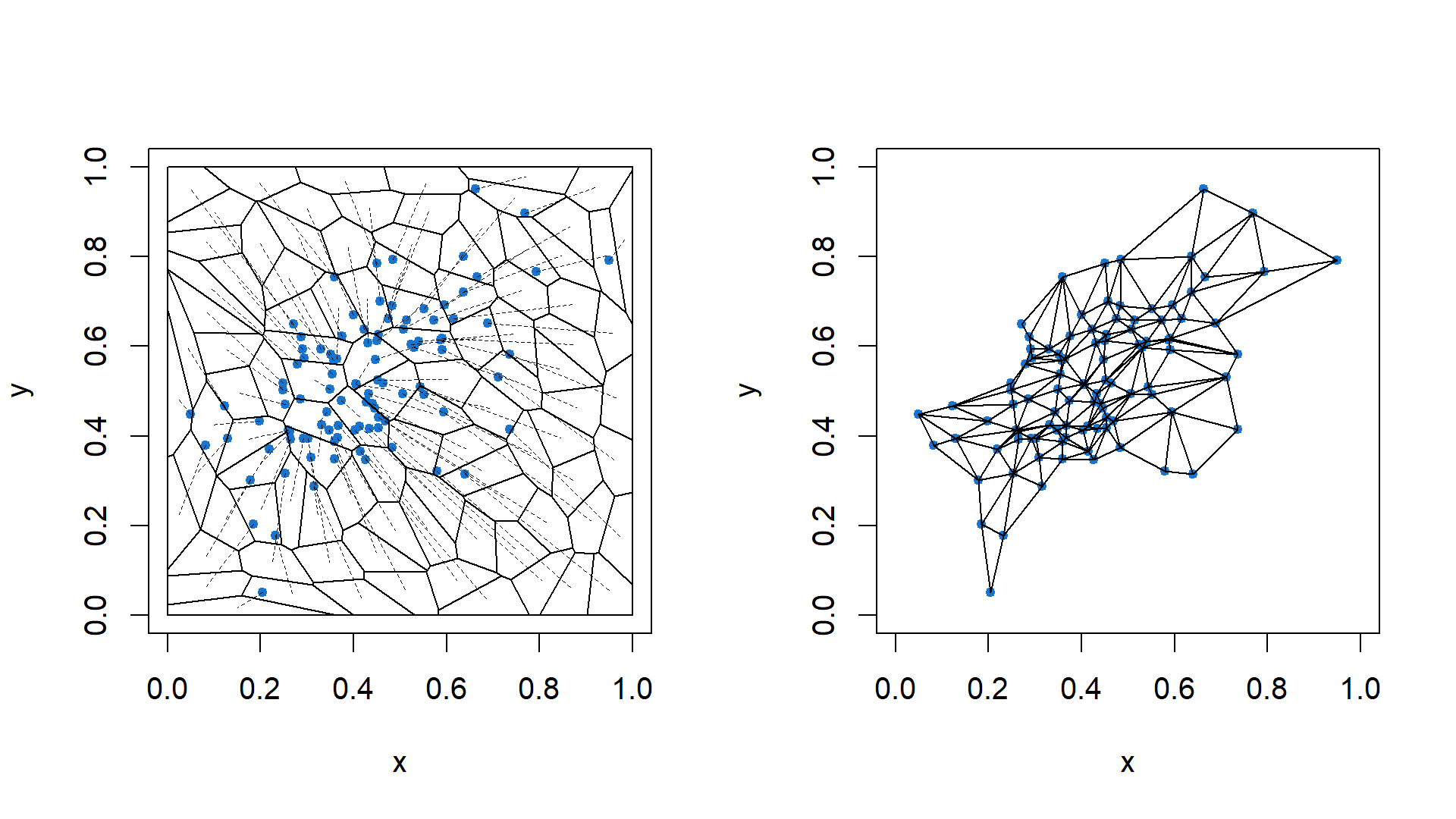
# plot the restricted Voronoi diagram and the restricted Delaunay triangulation
par(mfrow = c(1, 2))
plot(X.OTM, which = "Both", draw.center = F, draw.map = T)
Acknowledgment
The author is extremely grateful to Prof. Bodhisattva Sen and his student Promit Ghosal for their guidance in the development of this package. The author would also like to thank Dr. Bruno Lévy for his assistance with the Geogram library, and the TraME team, whose Rgeogram package provides inspirations to the early build of this package.
Reference
- Aurenhammer, F. 1987. “Power Diagrams: Properties, Algorithms and Applications.” SIAM Journal on Computing 16 (1): 78–96. https://doi.org/10.1137/0216006.
- Brenier, Yann. 1991. “Polar Factorization and Monotone Rearrangement of Vector-Valued Functions.” Communications on Pure and Applied Mathematics 44 (4): 375–417. https://doi.org/10.1002/cpa.3160440402.
- Cheng, Siu-Wing, Tamal Krishna Dey, and Jonathan Richard Shewchuk. 2013. Delaunay Mesh Generation. Chapman; Hall/CRC.
- Chernozhukov, Victor, Alfred Galichon, Marc Hallin, and Marc Henry. 2017. “Monge–Kantorovich Depth, Quantiles, Ranks and Signs.” The Annals of Statistics 45 (1): 223–56. https://doi.org/10.1214/16-AOS1450.
- Ghosal, Promit, and Bodhisattva Sen. 2019. “Multivariate Ranks and Quantiles Using Optimal Transportation and Applications to Goodness-of-Fit Testing.” http://arxiv.org/abs/1905.05340.
- Inria, project ALICE-GRAPHYS. 2019. “Geogram: A Programming Library of Geometric Algorithms.” http://alice.loria.fr/software/geogram/doc/html/index.html.
- Lévy, Bruno. 2015. “A Numerical Algorithm for L2 Semi-Discrete Optimal Transport in 3D.” ESAIM: M2AN 49 (6): 1693–1715.n https://doi.org/10.1051/m2an/2015055.
- Lévy, Bruno. 2015. “Robustness and Efficiency of Geometric Programs The Predicate Construction Kit (PCK).” Computer-Aided Design. https://hal.inria.fr/hal-01225202.
- Lévy, Bruno, and Erica L. Schwindt. 2018. “Notions of Optimal Transport Theory and How to Implement Them on a Computer.” Computers & Graphics 72: 135–48. https://doi.org/10.1016/j.cag.2018.01.009.
- Liu, Yang, Wenping Wang, Bruno Lévy, Feng Sun, Dong-Ming Yan, Lin Lu, and Chenglei Yang. 2009. “On Centroidal Voronoi Tessellation–Energy Smoothness and Fast Computation.” ACM Transactions on Graphics 28 (4): Article 101. https://doi.org/10.1145/1559755.1559758.
- McCann, Robert J. 1995. “Existence and Uniqueness of Monotone Measure-Preserving Maps.” Duke Math. J. 80 (2): 309–23. https://doi.org/10.1215/S0012-7094-95-08013-2.
- Toth, Csaba D., Joseph O’Rourke, and Jacob E. Goodman, eds. 2017. Handbook of Discrete and Computational Geometry. 3rd ed. Chapman; Hall/CRC.
- Xin, Shi-Qing, Bruno Lévy, Zhonggui Chen, Lei Chu, Yaohui Yu, Changhe Tu, and Wenping Wang. 2016. “Centroidal Power Diagrams with Capacity Constraints: Computation, Applications, and Extension.” ACM Trans. Graph. 35 (6): 244:1–244:12. https://doi.org/10.1145/2980179.2982428.
